If we were to name the most powerful assumption of all, which leads one on and on in an attempt to understand life, it is that all things are made of atoms, and that everything that living things do can be understood in terms of the jigglings and wigglings of atoms. - Richard Feynman
why the simulations?
molecular dynamics simulations play a major role in drug discovery. while modeling atoms as simple particles moving through space may seem violently oversimplified, this is what is actually being done in MD sims (to surprisingly great effect). tiny changes in molecular shape and its movement can make or break a drug.
take for example antibiotic resistance; some bacteria evolve mutations in the β-lactamase enzyme, which are proteins that break down β-lactam antibiotics like penicillin. normally, scientists would get around this by designing inhibitors that bind to the active site of β-lactamase and neutralize its effects, letting the antibiotic to continue doing its thing. however, some newer mutations in the enzyme started resisting both the inhibitor and the antibiotic, but didn’t change at all in the crystallized snapshots. molecular dynamics simulations allowed us to view this enzyme in motion (as all proteins are not static objects; they move and change shape to match whatever they’re trying to bind with). this revealed that the mutation made the active site of the enzyme more promiscuous/flexible, which allowed it to bind to and therefore break down more variations of antibiotics.
imaging tools like x-ray crystallography or cryo-electron microscopy only give us a look at the protein structure in a single moment in time, but molecular dynamic sims shed light on its movement, too.
🔗Understanding the structural mechanisms of antibiotic resistance sets the platform for new discovery
similar methods are also used in semiconductor manufacturing (as, if you’re reading this you probably know, it would be convenient to investigate the effect of a new tool from the cheap comfort of your lab before sinking fractions of a million dollars into a new machine). they are, however, less common in this field than in biophysics as the applications are more niche and tightly focused. mesoscopic metrics like resistivity, roughness, and grain size could be investigated with the simulation of a few thousand atoms, but more detailed investigations of “large” structures (at least large in comparison to protein) would require millions and millions of atoms, and i am gpu poor. im not yet sure why people who have the hardware and the iq for this have not written grand scale simulations for this field though; i suppose i’ll find out when i start hitting roadblocks.
i’m going to go over the current code for the very very primitive start i currently have working, and tie it together in a neat architecture diagram at the end. you should refer to the public repo if you want to truly understand the code, it would be a bit much to paste it all into code blocks here.
why am i doing this?
i think it’s cool.
chamber.cpp and chamber.hpp
the chamber is just the simulation space, the min and max coordinates that the particles may occupy. for now, it is 2 dimensional and all sputtering and occurs within this boundary. next step will be to introduce a third dimension. the chamber boundary coordinates can be anywhere in the world space as defined by the user. this is because i’m accounting for the potential need to have mirrored coords later, it might prove easier to work on (-10,0) to (10,0) than (0,0) to (20,0). as far as the cell indices and particles are concerned though, the chamber origin is in the bottom left corner. in other words, cell grid is chamber-local.
most of the code is self-explanatory, it’s just spatial indexing. we need this in order to bin particles into cells to perform a neighbor-search algorithm later on for collision detection.
exciting functional highlights, in plain english:
takes the width and height of the chamber, and based on the cellSize parameter, computes the number of cells that will fit in each dimension. it also enforces a round number of cells into the chamber, with negligible error tolerance.
spits out cell index of a given coordinate or particle.
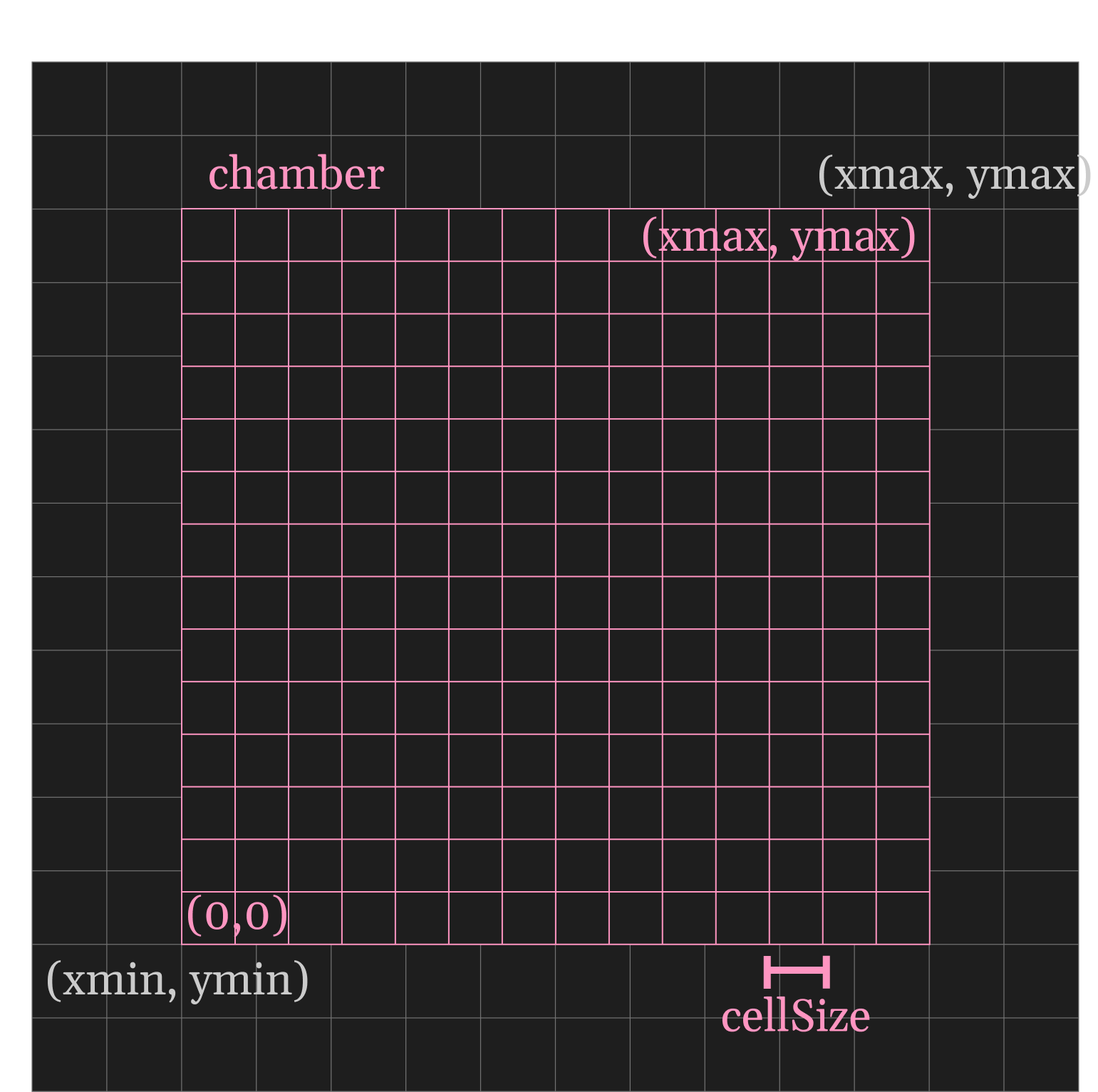world grid is independent of chamber grid!
a secret, third chamber file
one function relevant to the chamber is the boundary enforcement on a particle. simply, if a particle’s location is at the chamber boundary, it’s velocity will be mirrored depending on the boundary which it just hit. this is where we first touch gpu programming!!
we keep this function in a separate cuda header file because this function relies on particle data. all particle updates are done on the gpu, for obvious reasons. we want to minimize passing info between the cpu and gpu (host and device) because that bus is slow. also, there are likely going to be multiple collisions happening at the same time. if we tried to do all of them on the cpu, we’d build up a queue/lag, and that would make the simulation unrealistic (particles suspended waiting to be processed while their siblings proceed in the sim as normal) and slow.
particle.cpp
each particle has:
x,yx_prev,y_prev
>why not velocity?
that parameter is necessary if you’re using euler integration! euler int is a common object tracking method in game development, but it is less precise and prone to rounding error buildup. verlet integration, where you store the current and previous positions and use them to calculate velocity when necessary, allows for more stable and accurate motion; especially over many timesteps. it’s less sensitive to numerical drift.
in this implementation, we initialize particle positions at the top of the chamber, and give them randomized launch angles and speeds. the corresponding x_prev and y_prev are then back-calculated
by taking one step backward along their launch vector. this gives each particle an initial "memory" of where it came from, which verlet needs in order to compute the next position.
float speed = speedDist(rng);
float phi = angDist(rng);
float vx = speed * std::cos(phi);
float vy = speed * std::sin(phi);
update kernel
this is where we finally begin to use the two brain cells the stars above granted me, and also stray from classical molecular dynamics. when one is modeling a small body such as a protein, a couple thousand atoms suffice. this is not the case for a larger structure, such as a transistor or an interconnect, that we will be simulating here. it would be extremely computationally expensive to iterate through every single atom in the cell, check for a collision against every other atom in that cell (already (O)N^2), then compute the exact post-collision velocities for each. for the scale that we are working at, such precision is not necessary.collisions and the kinetic energy of a system not in equilibrium, and also when the gas is thin, can be adequately analyzed with statistics.
DSMC is a way to simulate how gases behave when the air is really thin, like at high altitudes or in a vacuum chamber. in these conditions, gas molecules are so far apart that they don't bump into each other very often. since collisions are both rare and inherently random, we can approximate them statistically without tracking each collision in detail. this doesn’t significantly affect the accuracy of properties like mean free path or energy distribution. however, free motion between collisions is predictable, and the final position of each particle matters, especially in processes like thin-film deposition. the spatial arrangement of deposited atoms can influence crystal structure, which in turn affects material properties like resistivity, adhesion, and efficiency. because of that, we need to track each particle’s position precisely, even if we approximate how they collide.
let us move forward with this assumption:
__global__
void rngInitKernel(curandState* states, int nCells, unsigned long seed) {
int idx = blockIdx.x * blockDim.x + threadIdx.x;
if (idx >= nCells) return;
curand_init(seed, idx, 0, &states[idx]);
}
void initRNGStates(curandState* states, int nCells, unsigned long seed) {
int threads = 256;
int blocks = (nCells + threads - 1) / threads;
rngInitKernel <<<blocks, threads>>>(states, nCells, seed);
cudaDeviceSynchronize();
}
here we have a CUDA kernel that initializes RNG (curandState) for each cell. each cell gets a thread and it's own RNG. individual RNGs are there because 1. separation lets me avoid correlated randomness (bad) 2. lets me avoid race conditions as if i had N cells trying to access the same RNG (also bad). the seed for each is the same yes, but the sequences will be different. generating separate seeds which in turn initialize separate RNGs is over the top.
the host-side/CPU funtion (the one not accompanied by the _global_ keyword) claims a standard 256 threads per block, rounds up the block number to ensure we have enough total threads for each cell, and calls the RNG kernel.
note:
_global_ is for a kernel called from the CPU (host). _device_ is for kernels only called from the GPU (device)
__global__
void collideDSMC(
Particle* ps,
int* particleIndices,
int* cellStart,
int* cellEnd,
curandState* states,
float dt,
float sigma,
float Vcell,
float maxRelSpeed
)
this kernel estimates collisions between particles in each spatial cell using the Direct Simulation Monte Carlo (DSMC) method. each thread handles one cell, and randomly samples particle pairs inside that cell to determine if a collision happens. the setup is self-explanatory.
int nPairs = int(0.5f * np * (np - 1) * sigma * dt / Vcell + 0.5f);
curandState& st = states[cell];
0.5f * np * (np - 1) is the total number of unique unordered pairs in a cell. this is the max amount of possible collisions within a cell.
once we know this, we scale it according to our physical constraints to make it more accurate:
let us talk about how we get this formula.
each particle has its own sphere of influence (force field). as it moves through space, that sphere sweeps through too creating an effective cyllinder of influence. the size of that cyllinder is obviousy
diameter of sphere of influence * relative velocity * time step
>why relative velocity? absolute velocity is irrelevant, two cars travelling 60mph in the same direction they will never collide (except if the drivers are two californians)
multiplying by particle density N gives the expected number of particle partners in that volume, which when combined with the cylinder volume swept per particle and the pair count gives us the expected collision rate. since we only have 1 species of particle so far, this turns to N*N. also, since collision between A and B is the same as B and A, we want to negate the doubles and so divide the total probability by 2.
thus,
R = 0.5 * N² * ⟨σ v_rel⟩
expected collisions = number of pairs × probability per pair = 0.5 * np * (np - 1) * σ * v_rel * dt / Vcell
note: this is the point at which i am questioning my intent to build this program in chunks of increasing complexity. i know similar simulations are performed with a dt of a femtosecond over a time period of micro to nanoseconds. should i simply set that now? will that be easily variable down the line when i add more complexity to this program? the dimensions of the chamber are meaningless digits now, i will have to relate the chamber dimension to particle sigma so that there's some actual meaning behind their relative size. if i dont, i might as well be simulating tennis balls flying around a room.
note 2: as i've discussed, statistical approximation of collisions here is appropriate and utilized in programs simulating larger counts of particles. however, my limitation here is the fact that all this maths only works on inert gasses. inert particles do behave like billard balls. straight lines are easy to track and approximate. however, in situations like plasma-enhanced PVD, or CVD where particles bond and interact by more rules than just Newtonian, we lose the inert advantage. ions and magnets bend and twist my simple, straight paths, and i'm not sure about the extent i can take statistical approximations to in this scenario. i sure as hell cant calculate rounded trajectories for a million atoms at a time, unless you have a couple of 4090s to throw my way.
this is getting long, i'll divide this up into parts for now. next up:
- what do we do with
nPairs - how do we randomly select pairs?
- how do we compute if they actually collide?
- how do we update them if they do?